Monte-carlo tree search with deep Q function and online planning

Published: February 01, 2023 by Chia-Hsien (Cathy) Shih

Extensions of the monte-carlo tree search (MCTS) in this tutorial
- instead of tabular Q function, use NN-approximated Q function for broader applications (can take continuous states)
- instead of planning form root at once and extract the learned policy, modify the code to plan online.
  - The advantage is that we don’t need to visit every state and learn the whole picture. We just quickly perform suboptimal actions that can get things done.
- allow pre-trained Q to guide the tree search
Analysis on performances in a simple grid world

Online planning with MCTS

MCTS builds up a tree (previous notes)
- state-node layer and action-node layer alternatively
- procedure
  - select a state node that is not fully expanded
  - expand the selected node by trying an action (randomly) and get the next state node
  - simulate from s’ till a termination state
  - backpropagate the return
To do online planning and more efficient search, I modify the following steps:
- expand with bandit algorithms instead of random actions
- simulate only till a limited depth
  - it is inefficient to always simulate to the end for every node
  - to calculate the accumulated reward, use the approximated q for the rest of the episode

test case: grid world
- start at left bottom (0,0)
- goal: reach (3,2)
- action: moving in four directions
performance analysis is over 5 trials

I call the original code “offline” because
- the agent is placed at the initial state without any prior knowledge (of the world or the pre-trained Q), it has to
  - build the tree
  - while searching from the root over and over again
    - update Q function
    - until the predefined timeout
- the policy is extracted at the end
timeout 2.5
- success: 1 out of 5 trials
- time spent (from building the tree to update Q):
  - time spent 2.5152747631073
  - time spent 2.6165850162506104
  - time spent 2.5032870769500732
  - time spent 2.503243923187256
  - time spent 2.5086100101470947
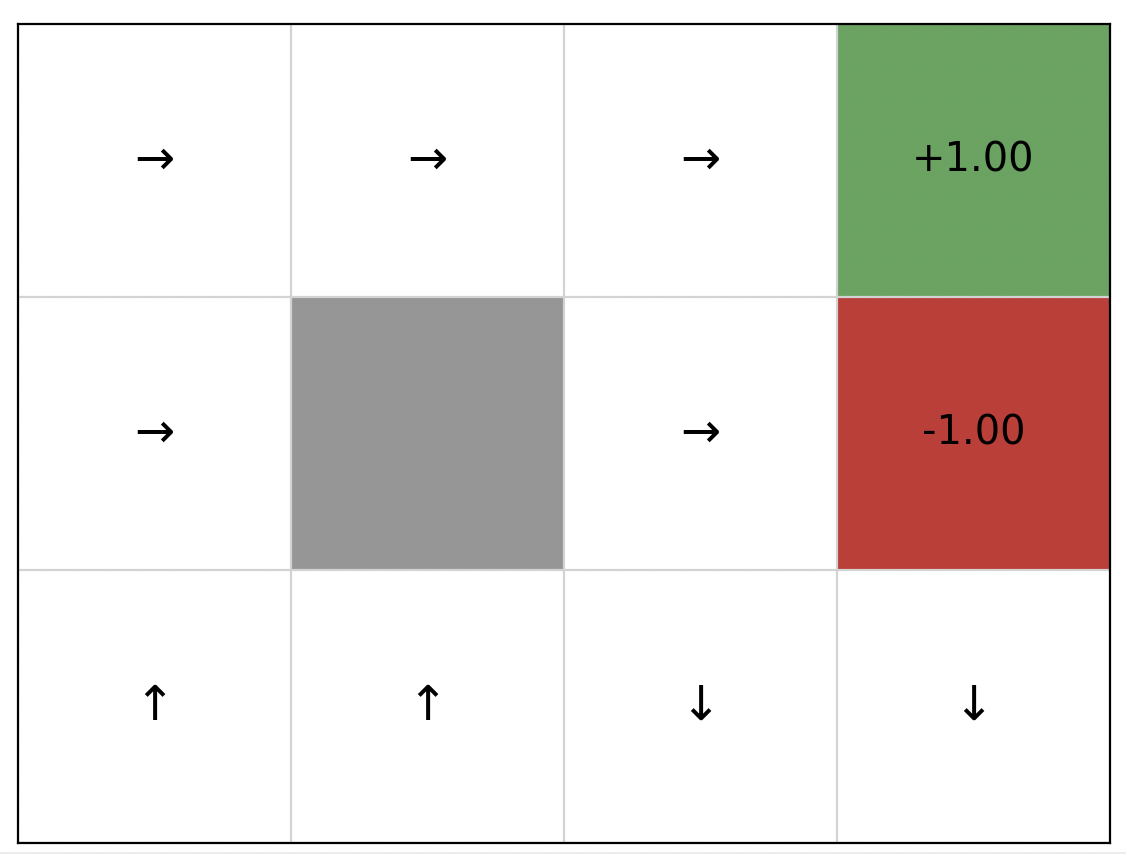
- one failing example
  - the first few layers of the tree
  - the extracted policy can't lead the agent to the goal
timeout 5
- success: 5 out of 5 trials
- time spent:
  - time spent 5.0320940017700195
  - time spent 5.042095184326172
  - time spent 5.0121259689331055
  - time spent 5.012312173843384
  - time spent 5.088823080062866
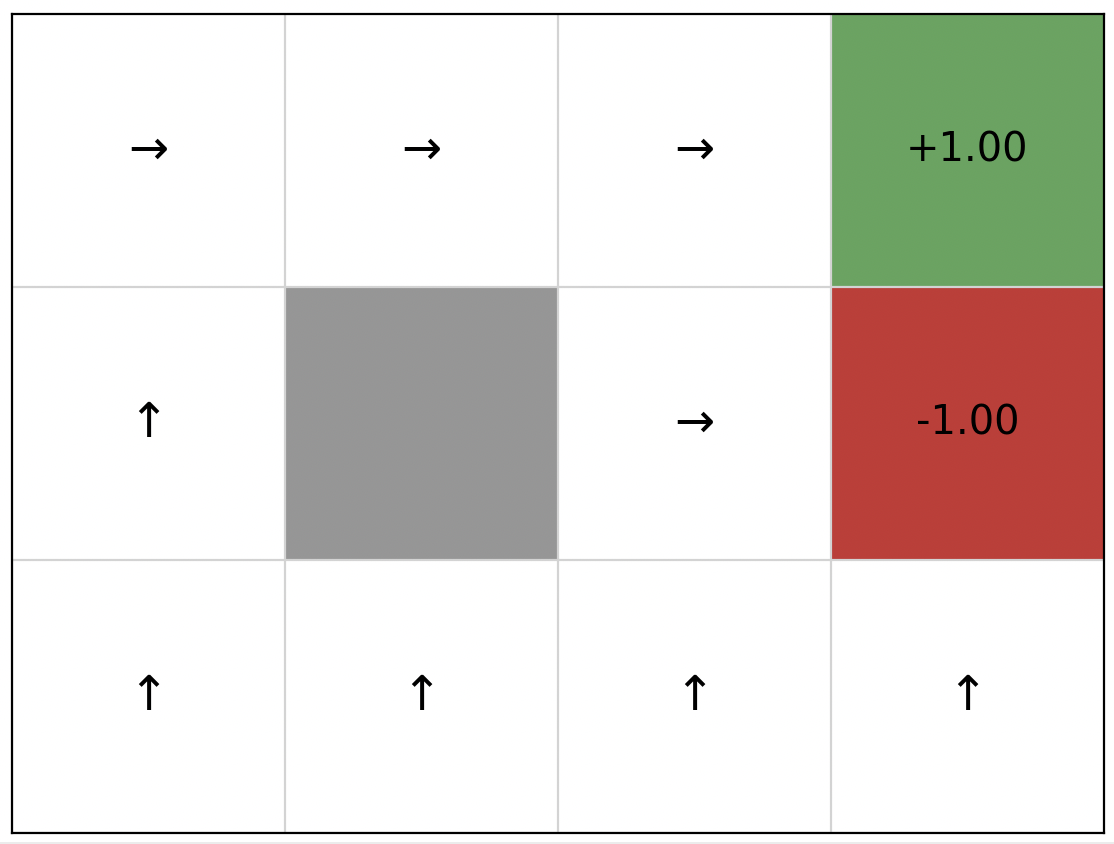
- example
  - the first few layers of the tree
  - the extracted policy leads the agent to the goal
This approach takes longer to extract a consistent policy because
- requires visiting all the states a lot of times to train the NN-approximated Q fn
- the variance is high because the training is in monte-carlo style
another disadvantage: only when the extracted policy is perfect, the agent can start using it

analysis follows most of the approaches set in the last section. To accommodate the online fashion, the trails is performed with these variables
- tree limit: only build the tree till depth=3 (o.w. it’s just offline)
- simulation depth: instead of Monte Carlo simulation, look ahead only for this many steps
- pre-trained Q
online planning can give policy like
- (0, 0) ►(1, 0) ►(2, 0) ▼(2, 0) ▼(2, 0) ◄(1, 0) ◄(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ▼(0, 0) ◄(0, 0) ◄(0, 0) ◄(0, 0) ◄(0, 0) ◄(0, 0) ►(1, 0) ◄(0, 0) ◄(0, 0) ►(1, 0) ◄(0, 0) ►(1, 0) ▲(1, 0) ◄(0, 0) ▲(0, 1) ▲(0, 2) ◄(0, 2) ◄(0, 2) ◄(0, 2) ▼(0, 1) ▲(0, 2) ▼(0, 1) ►(0, 1) ▲(0, 2) ◄(0, 2) ►(1, 2) ►(2, 2) ►goal
- what the agent does is not optimal, but planning online can lead the agent to the goal earlier than the offline method as shown below
- in real-world application, we can constrain the robot’s motions (not performing the action that is not safe e.g. going towards the wall)

depth = 3
- success 5 out of 5 trials, average time 3.04
  - time spent 0.5703649520874023
  - time spent 3.430715799331665
  - time spent 3.38307785987854
  - time spent 5.041029930114746
  - time spent 2.761559247970581
depth = 5
- success 5 out of 5 trials, average time 2.04
  - time spent 0.2971813678741455
  - time spent 0.7031919956207275
  - time spent 7.24423885345459
  - time spent 0.44618701934814453
  - time spent 1.539870262145996
conclusion
- planning online can lead the agent to the goal (2.04s / 3.04s) earlier than the offline method (5s)
  - picking the right tree limit is crucial to balance the performance and the time cost
- in worst case scenario it can take longer than the offline method, especially for this simple grid example
  - because the agent does action online and can keep visiting the few same states when the Q function is not converging or approximated fast enough

methods
- perfect pre-trained Q (baseline)
  - train for 100 eps (retrain for each trials)
  - the extracted policy is optimal and the q function is relatively easier to compare between actions
- pre-trained Q for only 5 eps
  - the extracted policy is not optimal and the q function is relatively not comparable between actions
result
- perfect pre-trained Q
  - success 5 out of 5 trials, average time 0.90 - time spent 0.4416477680206299 - time spent 0.6683788299560547 - time spent 1.6460108757019043 - time spent 0.713360071182251 - time spent 1.0494542121887207
- pre-trained Q for only 5 eps
  - success 5 out of 5 trials, average time 0.77
    - time spent 0.5686788558959961
    - time spent 0.54811692237854
    - time spent 1.0325219631195068
    - time spent 0.2939751148223877
    - time spent 1.4327030181884766
using pre-trained models, we can get the agent to the goal with faster online planning
- pre-training is extra work and time, but here the results show that
  - the pre-trained model does NOT need to be perfect in terms of the extracted policy and approximated values
  - the pre-training does NOT need good experiences, any kinds of experiences can be good for later planning
    - in one trial, the agent ended in the trap for all the five episodes, nevertheless, the online planning is able to get the agent to the goal faster than without any experience.