Spatial Action Maps and FlingBot for Cloth Unfolding

Published: by Creative Commons Licence

Dynamic manipulation

  • e.g. fling and throw motions in daily life
  • why dynamic manipulation?
    • efficient (high velocity)
    • expand physical reach range
    • → single-arm quasi-static actions
      • require more interactions for bad initial configurations (crumpled clothes)
      • limit maximum cloth size
  • goal: use dual-arm robot to unfold from arbitrary initial configurations
  • method
    • self-supervised learning
    • primitives: pick → stretch → fling
  • result
    • novel rectangular cloths (require only 3 actions to reach 80% coverage)
    • clothes larger than system's reach range
    • T-shirts
    • real-world transfer → 4x coverage than the quasi-static baseline
  • quasi-static manipulation → pick and drag actions
    • friction models
      • hard to estimate in real life
      • hard to be derived from visual inputs
    • reinforcement learning with expert demonstrations
    • identify key points (wrinkles, corners, and/or edges)
      • limitation: can not handle severely self-occluded configurations (crumpled clothes)
    • self-supervised learning
      • unfold → factorized pick and place actions
      • folding → goal conditioned using spatial action maps
  • → key differences in this work
    • visual input → no need of ground truth (motion capturing system)
    • self-supervised → no need of expert

Method

  • given two appropriate grasp points, the motion primitives should be sufficient for single step unfolding when possible
    • pick at two locations L, R with two arms → only problem here
    • stretch (unfold in one direction)
      • lift the cloth to 0.30m and stretch the cloth taut in between them
    • fling (unfold in the other direction)
      • fling the cloth forward 0.70m at 1.4m s−1 then pull backwards 0.50m at 1.4m s−1
      • advantages
        • a simpler policy (fling action can effectively unfold many clothes) which generalizes better to different cloth types
        • reach higher coverages in smaller numbers of interactions
        • manipulate clothes larger than the system’s reach range
  • problem constraints
    • two picking points L and R are in R^2 because we know depth
      • two pixels from visual inputs
    • L is left of R
    • grasp width has to satisfy system limit and safe distance
    • → parameterize with center point (C_x, C_y) and angle (theta) between -90 to 90 and grasp width (w)
  • value function
    • spatial action maps → recover values with varying scales and rotations in real-world space by varying the transformation applied to the visual inputs
      • visual input → batch of rotated and scaled data (predefined values) → predict batch of value maps
      • value map
        • each pixel value corresponds to the action value of that location (pixel index), rotations and scales.
    • predict the difference in coverage before and after the action
    • pick action based on the highest values among the maps (to get max coverage)
  • self-supervised learning
    • train end-to-end in simulation → finetune in the real world

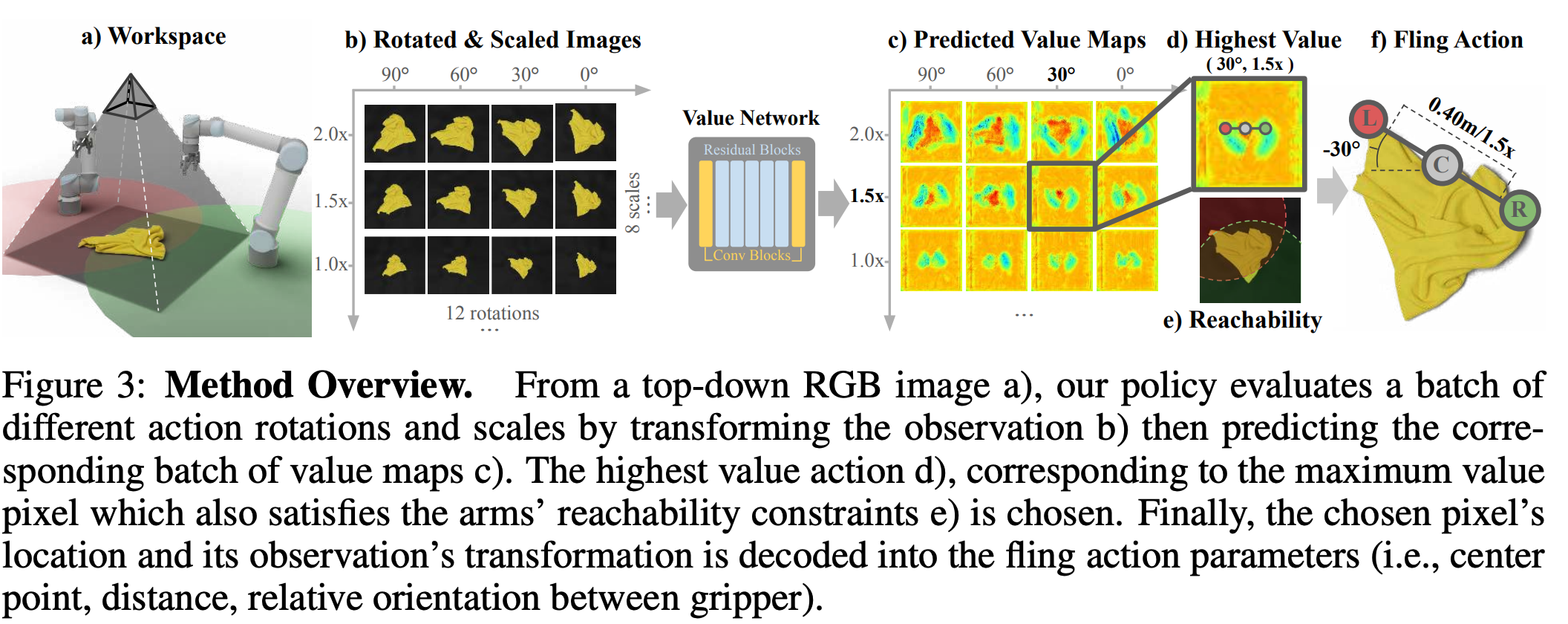
flingbot

Spatial action map

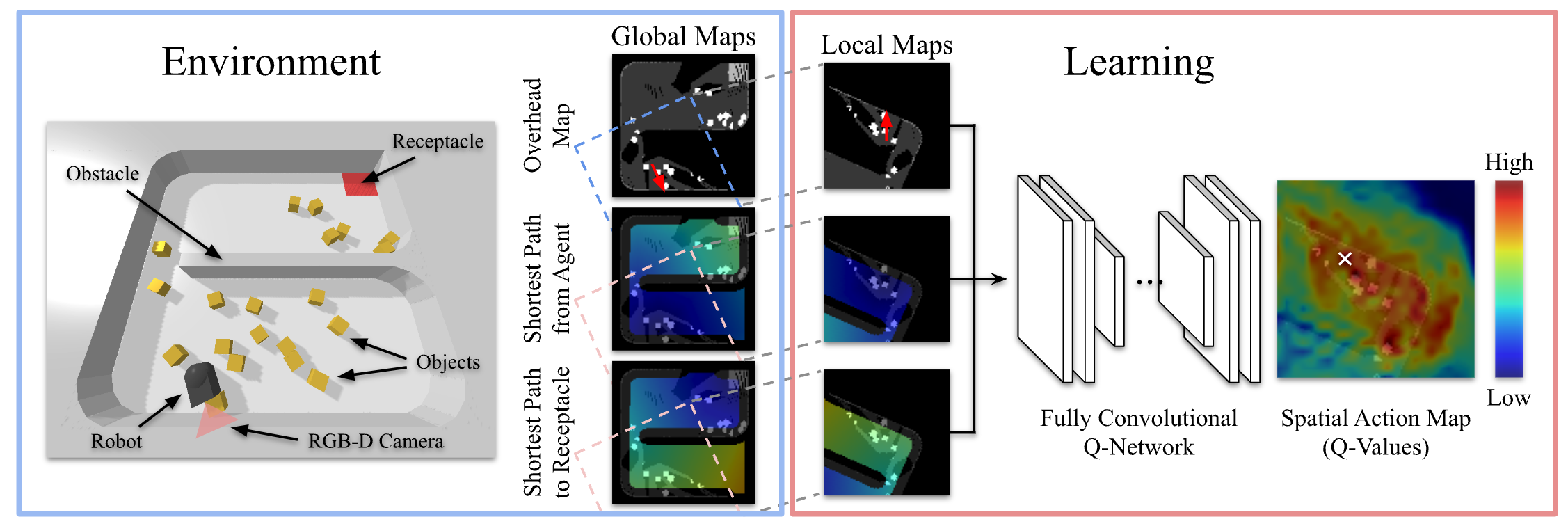
  • state:
    • robot is positioned in the center of each image and looking along the y axis
    • 4-channel image (robot's own visual observations, GPS coordinates, local mapping, and task-related goal coordinates)
      • local observation (overhead image or reconstructed env)
      • robot position (masked image)
      • heatmap of the shortest path dist from agent to the pixel location
      • heatmap of the shortest path dist from receptacle to the pixel location
  • action:
    • pixel location in the action map &rarrl robot’s desired locations
    • a movement primitive is used to execute the move
  • limitations
    • high-level motion primitives
    • limit to tasks in 2D space

spatial action map

[1] Ha, Huy, and Shuran Song. "Flingbot: The unreasonable effectiveness of dynamic manipulation for cloth unfolding." Conference on Robot Learning. PMLR, 2022.

[2] Wu, Jimmy, et al. "Spatial action maps for mobile manipulation." arXiv preprint arXiv:2004.09141 (2020).